Scalar Electric Potential / Electrostatic Potential (V) - Electrostatic Fields.
- If a charge is placed in the vicinity of another charge (or in the field of another charge), it experiences a force.
- If a field being acted on by a force is moved from one point to another, then work is either said to be done on the system or by the system.
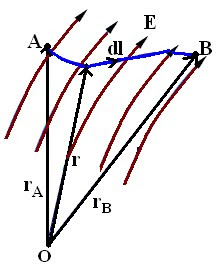
- Say a point charge Q is moved from point A to point B in an electric field E, then the work done in moving the point charge is given as:
WA→B = - ∫AB (F . dl) = - Q ∫AB(E . dl)
where the – ve sign indicates that the work is done on the system by an external agent.
- The work done per unit charge in moving a test charge from point A to point B is the electrostatic potential difference between the two points(VAB).
VAB = WA→B / Q
= - ∫AB(E . dl)
= - ∫InitialFinal (E . dl)
- If the potential difference is positive, there is a gain in potential energy in the movement, external agent performs the work against the field.
- If the sign of the potential difference is negative, work is done by the field.
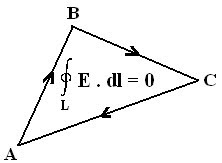
- The electrostatic field is conservative i.e. the value of the line integral depends only on end points and is independent of the path taken.
- Since the electrostatic field is conservative, the electric potential can also be written as:
VAB = - ∫AB (E . dl )
= - ∫APo (E . dl) - ∫ PoB (E . dl)
= - ∫PoB (E . dl) - (- ∫APo(E . dl)
= VB – VA
Thus the potential difference between two points in an electrostatic field is a scalar field that is defined at every point in space and is independent of the path taken.
- The work done in moving a point charge from point A to point B can be written as:
WA→B = - Q [VB – VA] = - Q ∫AB (E . dl)
- Consider a point charge Q at origin O.
- Now if a unit test charge is moved from point A to Point B, then the potential difference between them is given as:
- Electrostatic potential or Scalar Electric potential (V) at any point P is given by:
V = - ∫PoP (E . dl)
The reference point Po is where the potential is zero (analogues to ground in a circuit).
- The reference is often taken to be at infinity so that the potential of a point in space is defined as
V = - ∫∞P (E . dl)
- Basically potential is considered to be zero at infinity. Thus potential at any point ( rB = r) due to a point charge Q can be written as the amount of work done in bringing a unit positive charge from infinity to that point (i.e. rA → ∞)
- Electric potential (V) at point r due to a point charge Q located at a point with position vector r1 is given as:
- Similarly for N point charges Q1, Q2 ….Qn located at points with position vectors r1, r2, r3…..rn, the electric potential (V) at point r is given as:
- The charge element dQ and the total charge due to different charge distribution is given as:
dQ = ρldl → Q = ∫L (ρldl) → (Line Charge)
dQ = ρsds → Q = ∫S (ρsds) → (Surface Charge)
dQ = ρvdv → Q = ∫V (ρvdv) → (Volume Charge)
ALSO READ:
- Gauss's Law - Theory.
- Gauss's Law - Application To a Point charge.
- Gauss's Law - Application To An Infinite Line Charge.
- Gauss's Law - Application To An Infinite Sheet Charge.
- Gauss's Law - Application To a Uniformly Charged Sphere.
- Numericals / Solved Examples - Gauss's Law.
- Scalar Electric Potential / Electrostatic Potential (V).
- Relationship Between Electric Field Intensity (E) and Electrostatic Potential (V).
- Electric Potential Due To a Circular Disk.
- Electric Dipole.
- Numericals / Solved Examples - Electric Potential and Electric Dipole.
- Energy Density In Electrostatic Field / Work Done To Assemble Charges.
- Numericals / Solved Examples - Electrostatic Energy and Energy Density.
- Numericals / Solved Examples - Gauss's law...
Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.









Comments
Post a Comment