Gauss Law (Theory) & Application To A Point Charge - Field Theory.



- Gauss law is one of the fundamental laws of Electrostatics.


- It states that
“The net electric flux emanating or coming from a close surface S is equal to the total charge contained within the volume V bounded by that surface.”

We know,

Therefore
Ψ = Qenc


Hence Gauss law also states that
 “The total electric flux Ψ through any closed surface is equal to the enclosed electric charge.”


- Charge contained in a volume is given as:
dQ = ρv dv → Q = ∫V ρv dv


Hence we have,



 


Applying Divergence theorem we have,








Comparing the above two equations, we have







And hence 
∇ . D = ρv


This equation is called the 1st Maxwell's equation of electrostatics.


- Gauss law is an easy way of finding electric field for some symmetric problems in electrostatics.


- Gauss law relates the electric field at points on a closed Gaussian surface to the net charge enclosed by that surface.


- One thing to remember is Qenc contains charges which are enclosed within the volume. Charges outside the volume, no matter how large or how close it may be, are not included in the term Qenc.



Procedure To Apply Gauss Law:

- Check out whether symmetric charge distribution exists or not.


- If yes, a hypothetical surface called a Gaussian surface is selected such that E / D (due to charge) is either normal or tangential to the Gaussian surface.


- Gaussian surface is a hypothetical (any imaginary) closed surface enclosing the charge configuration.


- Gaussian surface is a surface to which the electric flux density is normal and over which equal to a constant value.



Application Of Gauss Law To A Point Charge:


- Consider a point charge Q at the origin, say at point P, the electric flux density (D) is to be evaluated.


- Gaussian Surface selected for a point charge is a sphere centered at origin.

From the diagram its clear that


- Electric flux density is everywhere normal to the Gaussian surface i.e. D = Dr ar


- The total charge enclosed by the Gaussian surface, Qenc = Q.


- Since the Gaussian surface is a hollow sphere, hence the variable terms are θ and φ. Thus the differential surface for a hollow sphere is given as:

ds = ∫(φ=0)2π ∫(θ=0)π  (r2 sinθ dθ dφ) ar = 4πr2 ar


- Hence applying gauss law, we have







→ Qenc = Dr 4πr2


Hence

Again we know that, D = ε E.

Therefore




ALSO READ: 

- Gauss's Law - Theory.

- Gauss's Law - Application To a Point charge.

- Gauss's Law - Application To An Infinite Line Charge.

- Gauss's Law - Application To An Infinite Sheet Charge.

- Gauss's Law - Application To a Uniformly Charged Sphere.

- Numericals / Solved Examples - Gauss's Law.

- Scalar Electric Potential / Electrostatic Potential (V).

- Relationship Between Electric Field Intensity (E) and Electrostatic Potential (V).

- Electric Potential Due To a Circular Disk.

- Electric Dipole.

- Numericals / Solved Examples - Electric Potential and Electric Dipole.

- Energy Density In Electrostatic Field / Work Done To Assemble Charges.

- Numericals / Solved Examples - Electrostatic Energy and Energy Density.

- Numericals / Solved Examples - Gauss's law...


- Short Notes/FAQ's

Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.

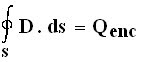
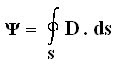
Comments

Post a Comment

Popular posts from this blog

Circular Cylindrical Coordinate System (ρ, φ, z) - Field Theory.

Image
A Vector in Cylindrical system is represented as (A ρ , A φ , A z ) or A = A ρ a ρ + A φ a φ + A z a z Where a ρ , a φ and a z are the unit vectors in ρ, φ and z direction respectively. The physical significance of each parameter of cylindrical coordinates:      - The value ρ indicates the distance of the point from the z-axis. It is the radius of the cylinder .      - The value φ, also called the azimuthal angle , indicates the rotation angle around the z-axis. It is basically measured from the x axis in the x-y plane. It is measured anti-clockwise.      - The value z indicates the distance of the point from z-axis. It is the same as in the Cartesian system. In short, it is the height of the cylinder. Range of the variables: It defines the minimum and the maximum value that ρ, φ and z can have in Cartesian system.  0 ≤ ρ ≤ ∞  0 ≤ φ ≤ 2π - ∞ ≤ z ≤ ∞   Figure shows Point P and Unit vectors in Cyli...
Read More »

Electric Field Intensity (E) Due To a Circular Ring Charge - Field Theory.

Image
- Consider a circular ring of radius 'a' which carries a uniform line charge density ρ L as shown in figure. - We need to find out electric field at a point P (0, 0, h) on the z axis (z > 0). - Electric field intensity (E) due to any line charge (ρ L ) in general is given as: In this case, dl = a dφ (Since the differential part dl is a differential arc ) R 2 = a 2 + h 2 Consider the triangle shown in the above figure a a ρ + R = h a z → R = - a a ρ + h a z a R = R / | R | a R = - a a ρ + h a z / ( a 2 + h 2 ) 1/2 Substituting all these values in the above equations, the electric field intensity E becomes: - For every element dl there is a corresponding element diametrically opposite that gives an equal but opposite dE ρ so that the two contributions cancel each other. Hence contribution along a ρ due to symmetry adds up to zero. - Therefore the final electric field intensity at point (0, 0, h) has ...
Read More »

Electric Potential (V) Due To A Uniformly Charged Circular Disc - Field Theory.

Image
- Consider a circular disc of radius ‘a’ which carries a uniform surface charge density ρ s , C /m 2 . - Say the disk lies on x - y plane (or z = 0 plane) with its axis along the z axis as shown in the figure. - We need to find out electric potential (V) due to a circular disk at a point P (0, 0, h) on the z axis (z > 0). - Electric potential (V) at a point due to any surface charge (ρ s ) is given as: - In this case, ds = ρ dρ dφ (Since it’s a disc, the varying terms are radius ρ and angle φ ) R = (ρ 2 + h 2 ) 1/2 - Hence electric potential (V) is given as: - On solving further the equation becomes - As a → 0 , electric potential (V) also tends to zero i.e. V → 0. - Hence the electric potential at point (0, 0, h) is given as: ALSO READ:  - Gauss's Law - Theory. - Gauss's Law - Application To a Point charge. - Gauss's Law - Application To An Infinite Line Charge. - Gauss's ...
Read More »