Energy Density In Electrostatic Field / Work Done To Assemble Charges.


- In case, if we wish to assemble a number of charges in an empty system, work is required to do so.


- Also electrostatic energy is said to be stored in such a collection.


- Let us build up a system in which we position three point charges Q1, Q2 and Q3 at position r1, r2 and r3 respectively in an initially empty system.


- Consider a point charge Q1 transferred from infinity to position r1 in the system. It takes no work to bring the first charge from infinity since there is no electric field to fight against (as the system is empty i.e. charge free).

Hence, W1 = 0 J


- Now bring in another point charge Q2 from infinity to position r2 in the system. In this case we have to do work against the electric field generated by the first charge Q1.

Hence, W2 = Q2 V21

where V21 is the electrostatic potential at point r2 due to Q1.


- Work done W2 is also given as:



- Now bring in another point charge Q3 from infinity to position r3 in the system. In this case we have to do work against the electric field generated by Q1 and Q2.


Hence, W3 = Q3 V31 + Q3 V32 = Q3 ( V31 + V32 )

where V31 and V32 are electrostatic potential at point r3 due to Q1 and Q2 respectively.


- The work done is simply the sum of the work done against the electric field generated by point charge Q1 and Q2 taken in isolation: 




- Thus the total work done in assembling the three charges is given as:


WE = W1 + W2 + W3
                               = 0 + Q2 V21 + Q3 ( V31 + V32 )


- Also total work done ( WE ) is given as:




- If the charges were positioned in reverse order, then the total work done in assembling them is given as:

WE = W3 + W2+ W1
                            = 0 + Q2V23 + Q3( V12+ V13)

where V23 is the electrostatic potential at point r2 due to Q3 and V12 and V13 are electrostatic potential at point r1 due to Q2 and Q3 respectively.


- Adding the above two equations we have,


2WE = Q1 ( V12 + V13) + Q2 ( V21 + V23) + Q3 ( V31 + V32)
                                          = Q1 V1 + Q2 V2 + Q3 V3


Hence
WE =1 / 2 [Q1V1 + Q2V2 + Q3V3]


where V1, V2 and V3 are total potentials at position r1, r2 and r3 respectively.


- The result can be generalized for N point charges as:




- The above equation has three interpretation:

          a) This equation represents the potential energy of the system.
  
          b) This is the work done in bringing the static charges from infinity and assembling them in the required system.
 
          c) This is the kinetic energy which would be released if the system gets dissolved i.e. the charges returns back to infinity.


- In place of point charge, if the system has continuous charge distribution ( line, surface or volume charge), then the total work done in assembling them is given as:



- Since ρv = ∇ . D and E = - ∇ V,

Substituting the values in the above equation, work done in assembling a volume charge distribution in terms of electric field and flux density is given as:

 

- The above equation tells us that the potential energy of a continuous charge distribution is stored in an electric field.


- The electrostatic energy density wE is defined as:


ALSO READ: 

- Gauss's Law - Theory.

- Gauss's Law - Application To a Point charge.

- Gauss's Law - Application To An Infinite Line Charge.

- Gauss's Law - Application To An Infinite Sheet Charge.

- Gauss's Law - Application To a Uniformly Charged Sphere.

- Numericals / Solved Examples - Gauss's Law.

- Scalar Electric Potential / Electrostatic Potential (V).

- Relationship Between Electric Field Intensity (E) and Electrostatic Potential (V).

- Electric Potential Due To a Circular Disk.

- Electric Dipole.

- Numericals / Solved Examples - Electric Potential and Electric Dipole.

- Energy Density In Electrostatic Field / Work Done To Assemble Charges.

- Numericals / Solved Examples - Electrostatic Energy and Energy Density.

- Numericals / Solved Examples - Gauss's law...


- Short Notes/FAQ's

Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.

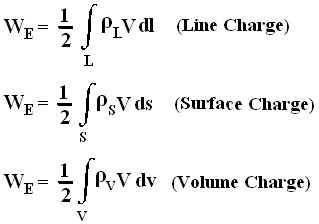
Comments

Post a Comment

Popular posts from this blog

Circular Cylindrical Coordinate System (ρ, φ, z) - Field Theory.

Image
A Vector in Cylindrical system is represented as (A ρ , A φ , A z ) or A = A ρ a ρ + A φ a φ + A z a z Where a ρ , a φ and a z are the unit vectors in ρ, φ and z direction respectively. The physical significance of each parameter of cylindrical coordinates:      - The value ρ indicates the distance of the point from the z-axis. It is the radius of the cylinder .      - The value φ, also called the azimuthal angle , indicates the rotation angle around the z-axis. It is basically measured from the x axis in the x-y plane. It is measured anti-clockwise.      - The value z indicates the distance of the point from z-axis. It is the same as in the Cartesian system. In short, it is the height of the cylinder. Range of the variables: It defines the minimum and the maximum value that ρ, φ and z can have in Cartesian system.  0 ≤ ρ ≤ ∞  0 ≤ φ ≤ 2π - ∞ ≤ z ≤ ∞   Figure shows Point P and Unit vectors in Cyli...
Read More »

Electric Field Intensity (E) Due To a Circular Ring Charge - Field Theory.

Image
- Consider a circular ring of radius 'a' which carries a uniform line charge density ρ L as shown in figure. - We need to find out electric field at a point P (0, 0, h) on the z axis (z > 0). - Electric field intensity (E) due to any line charge (ρ L ) in general is given as: In this case, dl = a dφ (Since the differential part dl is a differential arc ) R 2 = a 2 + h 2 Consider the triangle shown in the above figure a a ρ + R = h a z → R = - a a ρ + h a z a R = R / | R | a R = - a a ρ + h a z / ( a 2 + h 2 ) 1/2 Substituting all these values in the above equations, the electric field intensity E becomes: - For every element dl there is a corresponding element diametrically opposite that gives an equal but opposite dE ρ so that the two contributions cancel each other. Hence contribution along a ρ due to symmetry adds up to zero. - Therefore the final electric field intensity at point (0, 0, h) has ...
Read More »

Electric Potential (V) Due To A Uniformly Charged Circular Disc - Field Theory.

Image
- Consider a circular disc of radius ‘a’ which carries a uniform surface charge density ρ s , C /m 2 . - Say the disk lies on x - y plane (or z = 0 plane) with its axis along the z axis as shown in the figure. - We need to find out electric potential (V) due to a circular disk at a point P (0, 0, h) on the z axis (z > 0). - Electric potential (V) at a point due to any surface charge (ρ s ) is given as: - In this case, ds = ρ dρ dφ (Since it’s a disc, the varying terms are radius ρ and angle φ ) R = (ρ 2 + h 2 ) 1/2 - Hence electric potential (V) is given as: - On solving further the equation becomes - As a → 0 , electric potential (V) also tends to zero i.e. V → 0. - Hence the electric potential at point (0, 0, h) is given as: ALSO READ:  - Gauss's Law - Theory. - Gauss's Law - Application To a Point charge. - Gauss's Law - Application To An Infinite Line Charge. - Gauss's ...
Read More »