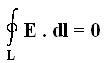ElectroMagnetic Theory Concepts & Solved Numericals

- An electric dipole consists of two point charges of equal magnitude but of opposite sign and separated by a small distance. - Consider an electric dipole centered at origin and placed in z – axis as shown in the figure: - The potential (V) at point P is given as: - If the distance between the charges (d) is very small as compared to the distance of the point P from the origin i.e. If r >> d, r 2 – r 1 ≅ d cosθ ;           r 1 ≅ r 2 = r ;           r 1 r 2 ≅ r 2 Substituting the values in the above equation, the potential at point P becomes: - Electric field intensity (E) is the negative gradient of Electric Potential (V). Hence, - The expressions for electric potential (V) and field intensity (E) above are only valid for a dipole centered at the origin and aligned with the z-axis. - To determine the fields produced by any arbitrary location and alignment , we first need to define a new quantity p , called the Dipole Moment.

- Consider a circular disc of radius ‘a’ which carries a uniform surface charge density ρ s , C /m 2 . - Say the disk lies on x - y plane (or z = 0 plane) with its axis along the z axis as shown in the figure. - We need to find out electric potential (V) due to a circular disk at a point P (0, 0, h) on the z axis (z > 0). - Electric potential (V) at a point due to any surface charge (ρ s ) is given as: - In this case, ds = ρ dρ dφ (Since it’s a disc, the varying terms are radius ρ and angle φ ) R = (ρ 2 + h 2 ) 1/2 - Hence electric potential (V) is given as: - On solving further the equation becomes - As a → 0 , electric potential (V) also tends to zero i.e. V → 0. - Hence the electric potential at point (0, 0, h) is given as: ALSO READ:  - Gauss's Law - Theory. - Gauss's Law - Application To a Point charge. - Gauss's Law - Application To An Infinite Line Charge. - Gauss's

- The work done per unit charge in moving a test charge from point A to point B is the electrostatic potential difference between the two points(V AB ). V AB = V B - V A Similarly, V BA = V A – V B - Hence it’s clear that potential difference is independent of the path taken. Therefore V AB = - V BA V AB + V BA = 0 - ∫ A B (E . dl) + [ - ∫ B A (E . dl) ] = 0 - The above equation shows that the line integral of Electric field intensity (E) along a closed path is equal to zero. - In simple words, “No work is done in moving a charge along a closed path in an electrostatic field”. - Applying Stokes’ Theorem to the above Equation, we have: - If the Curl of any vector field is equal to zero , then such a vector field is called an Irrotational or Conservative Field. - Hence an electrostatic field is also called a conservative field. - The above equation is called the second Maxwell’s Equation of Electrostatics. - Since Electric pot

- If a charge is placed in the vicinity of another charge (or in the field of another charge), it experiences a force. - If a field being acted on by a force is moved from one point to another, then work is either said to be done on the system or by the system. - Say a point charge Q is moved from point A to point B in an electric field E , then the work done in moving the point charge is given as:   W A→B = - ∫ A B (F . dl) = - Q ∫ A B (E . dl) where the – ve sign indicates that the work is done on the system by an external agent. - The work done per unit charge in moving a test charge from point A to point B is the electrostatic potential difference between the two points(V AB ). V AB = W A→B / Q  = - ∫ A B (E . dl)  = - ∫ Initial Final (E . dl) - If the potential difference is positive , there is a gain in potential energy in the movement, external agent performs the work against the field. - If the sign of the potential difference is negati

Q.1 A point charge of 30 nC is located at the origin while plane y = 3 carries charge 10 nC / m 2 . Find D at (0, 4, 3)? Ans: Electric flux density (D) at point (0, 4, 3) due to a point charge and line charge is given as: D = D Q + D ρ = 0.019 (0, 4, 3) + 5a y = 0.76 a y + 0.057 a z + 5a y = 5.076 a y + 0.057 a z Q.2 A charge distribution in free space has ρ v = 2r nC / m 3 for 0 < r < 10 m and zero otherwise. Determine E at r = 2m and r = 12m? Ans: Gauss’s law states that: For 0 ≤ r ≤ 10 D r (4πr 2 ) = ∫ ∫ ∫ 2r (r 2 sinθ dr dθ dφ) D r (4πr 2 ) = 4π (2r 4 ) / 4 For r ≥ 10 D r (4πr 2 ) = ∫ ∫ ∫ 2r o (r 2 sinθ dr dθ dφ) D r (4πr 2 ) = 4π (2r o 4 ) / 4 D r (4πr 2 ) = 2πr o 4 Q.3 If D = (2y 2 + z)a x + 4xy a y + x a z C/m 2 , find a) Volume charge density at (-1, 0, 3) b) The flux through the cube defined by 0 ≤ x ≤ 1, c) The total charge enclosed by the cube.  Ans: a) Vol

- Consider a sphere of radius “a” having a uniform volume charge density of ρ o C/m 3 . - Gaussian surface selected for a symmetric sphere charge is a sphere itself. - Here we consider two cases: A Gaussian surface with a radius r < a. A Gaussian surface with a radius r > a. CASE 1: If r < a (consider the 1st figure), the total charge enclosed by the Gaussian surface is: Electric flux is given as: Here ds is taken to be a function of θ and φ ( since the surface is a hollow sphere). Gauss law states that Ψ = Q enc Therefore, D r 4π r 2 = (4 / 3) (ρ o πr 3 )               Or D = (r / 3) ρ o a r (0 < r < a)  CASE II:  If r > a (consider the above figure), the total charge enclosed by the Gaussian surface is: Electric flux is given as:  Gauss law states that Ψ = Q enc Therefore, D r 4π r 2 = (4 / 3) (ρ o πa 3 )               Or D = (a 3 / 3r 2 ) ρ

- Consider an infinite line charge carrying a charge per unit length of ρ L along the z axis. - Gaussian surface selected for a symmetric line charge is a hollow cylinder of radius ρ and length l as shown in the figure - A cylinder has basically three surfaces: top, bottom and the curved cylindrical surface. From the diagram its clear that - Electric flux density (D)  is parallel to the top and bottom Gaussian surface. - Electric flux density (D) is normal to the curved cylindrical Gaussian surface. - Differential surface (ds) is always normal to a surface. D and ds are normal to each other for the top and bottom Gaussian surface. Hence ∫ (D . ds) = 0 Hence it’s clear that D and ds are parallel to each other only for the curvilinear Gaussian surface. - Since the Gaussian surface is a hollow cylinder , hence the variable terms are φ and z. Thus the differential surface for a hollow cylinder is given as: ds = ∫ (φ=0) 2π ∫ 0 l   (ρ dφ dz) a ρ

- Gauss law is one of the fundamental laws of Electrostatics. - It states that “The net electric flux emanating or coming from a close surface S is equal to the total charge contained within the volume V bounded by that surface.” We know, Therefore Ψ = Q enc Hence Gauss law also states that  “The total electric flux Ψ through any closed surface is equal to the enclosed electric charge.” - Charge contained in a volume is given as: dQ = ρ v dv → Q = ∫ V ρ v dv Hence we have,   Applying Divergence theorem we have, Comparing the above two equations, we have And hence   ∇ . D = ρ v This equation is called the 1 st Maxwell's equation of electrostatics. - Gauss law is an easy way of finding electric field for some symmetric problems in electrostatics. - Gauss law relates the electric field at points on a closed Gaussian surface to the net charge enclosed by that surface. - One thing to remember is Q enc