Application Of Gauss Law To A Uniformly Charged Sphere - Field Theory.


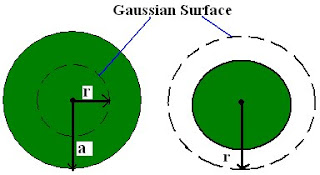
- Consider a sphere of radius “a” having a uniform volume charge density of ρo C/m3.


- Gaussian surface selected for a symmetric sphere charge is a sphere itself.


- Here we consider two cases:
  • A Gaussian surface with a radius r < a.
  • A Gaussian surface with a radius r > a.





CASE 1:

If r < a (consider the 1st figure), the total charge enclosed by the Gaussian surface is:











Electric flux is given as:













Here ds is taken to be a function of θ and φ( since the surface is a hollow sphere).


Gauss law states that Ψ = Qenc

Therefore,

Dr 4π r2 = (4 / 3) (ρo πr3)

              Or

D = (r / 3) ρo ar (0 < r < a) 



CASE II: 

If r > a (consider the above figure), the total charge enclosed by the Gaussian surface is:












Electric flux is given as:












 Gauss law states that Ψ = Qenc


Therefore,

Dr 4π r2 = (4 / 3) (ρo πa3)

              Or

D = (a3 / 3r2 ) ρo ar (r > a)


ALSO READ: 

- Gauss's Law - Theory.

- Gauss's Law - Application To a Point charge.

- Gauss's Law - Application To An Infinite Line Charge.

- Gauss's Law - Application To An Infinite Sheet Charge.

- Gauss's Law - Application To a Uniformly Charged Sphere.

- Numericals / Solved Examples - Gauss's Law.

- Scalar Electric Potential / Electrostatic Potential (V).

- Relationship Between Electric Field Intensity (E) and Electrostatic Potential (V).

- Electric Potential Due To a Circular Disk.

- Electric Dipole.

- Numericals / Solved Examples - Electric Potential and Electric Dipole.

- Energy Density In Electrostatic Field / Work Done To Assemble Charges.

- Numericals / Solved Examples - Electrostatic Energy and Energy Density.

- Numericals / Solved Examples - Gauss's law...



Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.

Comments

Post a Comment

Popular posts from this blog

Circular Cylindrical Coordinate System (ρ, φ, z) - Field Theory.

Image
A Vector in Cylindrical system is represented as (A ρ , A φ , A z ) or A = A ρ a ρ + A φ a φ + A z a z Where a ρ , a φ and a z are the unit vectors in ρ, φ and z direction respectively. The physical significance of each parameter of cylindrical coordinates:      - The value ρ indicates the distance of the point from the z-axis. It is the radius of the cylinder .      - The value φ, also called the azimuthal angle , indicates the rotation angle around the z-axis. It is basically measured from the x axis in the x-y plane. It is measured anti-clockwise.      - The value z indicates the distance of the point from z-axis. It is the same as in the Cartesian system. In short, it is the height of the cylinder. Range of the variables: It defines the minimum and the maximum value that ρ, φ and z can have in Cartesian system.  0 ≤ ρ ≤ ∞  0 ≤ φ ≤ 2π - ∞ ≤ z ≤ ∞   Figure shows Point P and Unit vectors in Cyli...
Read More »

Electric Field Intensity (E) Due To a Circular Ring Charge - Field Theory.

Image
- Consider a circular ring of radius 'a' which carries a uniform line charge density ρ L as shown in figure. - We need to find out electric field at a point P (0, 0, h) on the z axis (z > 0). - Electric field intensity (E) due to any line charge (ρ L ) in general is given as: In this case, dl = a dφ (Since the differential part dl is a differential arc ) R 2 = a 2 + h 2 Consider the triangle shown in the above figure a a ρ + R = h a z → R = - a a ρ + h a z a R = R / | R | a R = - a a ρ + h a z / ( a 2 + h 2 ) 1/2 Substituting all these values in the above equations, the electric field intensity E becomes: - For every element dl there is a corresponding element diametrically opposite that gives an equal but opposite dE ρ so that the two contributions cancel each other. Hence contribution along a ρ due to symmetry adds up to zero. - Therefore the final electric field intensity at point (0, 0, h) has ...
Read More »

Electric Potential (V) Due To A Uniformly Charged Circular Disc - Field Theory.

Image
- Consider a circular disc of radius ‘a’ which carries a uniform surface charge density ρ s , C /m 2 . - Say the disk lies on x - y plane (or z = 0 plane) with its axis along the z axis as shown in the figure. - We need to find out electric potential (V) due to a circular disk at a point P (0, 0, h) on the z axis (z > 0). - Electric potential (V) at a point due to any surface charge (ρ s ) is given as: - In this case, ds = ρ dρ dφ (Since it’s a disc, the varying terms are radius ρ and angle φ ) R = (ρ 2 + h 2 ) 1/2 - Hence electric potential (V) is given as: - On solving further the equation becomes - As a → 0 , electric potential (V) also tends to zero i.e. V → 0. - Hence the electric potential at point (0, 0, h) is given as: ALSO READ:  - Gauss's Law - Theory. - Gauss's Law - Application To a Point charge. - Gauss's Law - Application To An Infinite Line Charge. - Gauss's ...
Read More »