Solved Exercise/Numericals - Electric Potential, Potential Gradient & Electric Dipole.
Q.1 Determine the electric field due to the following potential:
a) V = x2 + 2y2 + 4z2
Ans:
= - (2x ax + 4y ay + 8z az )
= -2x ax - 4y ay - 8z az V/m
b) V = ρ2 (z + 1) sinφ
= - [ 2ρ (z + 1)sinφ aρ + ρ(z + 1) cosφ aφ + ρ2 sinφ az ]
= - 2ρ (z + 1)sinφ aρ - ρ(z + 1) cosφ aφ - ρ2 sinφ az
Q.2 A point charge of 5 nC is located at the origin. If V = 2v at (0, 6, -8), find
a) The potential at A (-3, 2, 6)
b) The potential at B (1, 5, 7)
c) The potential difference VAB
Ans:
If V (0, 6, -8) = 2 V
In this case
x = 0; y = 6; z = -8
Using the scalar relationship between Cartesian and spherical system, we have
r = (x2 + y2 +z2)1/2 = (100)1/2 =10
Hence
Electric potential at point r due to a point charge Q located at origin
→ C = - 2.5
a) Electric potential at point r due to a point charge Q located at a point (-3, 2, 6) is given as:
= 3. 929 V
b) Electric potential at point r due to a point charge Q located at a point (1, 5, 7) is given as:
= 2.696 V
c) The potential difference VAB is given as:
VAB = VB – VA = 2.696 – 3.929 = - 1.233 V
Q.3 If point charge 3 μC is located at the origin. Also there are two more charges -4 μC and 5 μC are located at (2, -1, 3) and (0, 4, -2) respectively. Find potential at (-1, 5, 2) ? Assume zero potential at infinity.
Ans:
For N point charges Q1, Q2 ….Qn located at points with position vectors r1, r2, r3…..rn, the electric potential at point r is given as:
At V ( ∞ ) = 0, C = 0
| r – r1 | = | (-1, 5, 2) – (2, -1, 3) | = (46)1/2
| r – r2 | = | (-1, 5, 2) – (0, 4, -2) | = (18)1/2
| r – r3 | = | (-1, 5, 2) – (0, 0, 0) | = (30)1/2
Hence electric potential is given as:
= 10.3 kV
Q.4 An electric dipole of 100 az pC.m is located at the origin. Find V and E at points
a) (0, 0, 10)
b) (1, π/3, π/2)
Ans:
a) At point (0, 0, 10)
Cartesian → Spherical
(x, y, z) → (r, θ, φ)
(0, 0, 10) → (10, 0o, 0o)
Electric potential (V) due to a electric dipole centered at origin and aligned with the z axis is written as:
Electric field intensity (E) is the negative gradient of Electric Potential (V).
b)At point (1, π/3, π/2)
Electric potential (V) due to a electric dipole centered at origin and aligned with the z axis is written as:
Electric field intensity (E) is the negative gradient of Electric Potential (V).
ALSO READ:
- Gauss's Law - Theory.
- Gauss's Law - Application To a Point charge.
- Gauss's Law - Application To An Infinite Line Charge.
- Gauss's Law - Application To An Infinite Sheet Charge.
- Gauss's Law - Application To a Uniformly Charged Sphere.
- Numericals / Solved Examples - Gauss's Law.
- Scalar Electric Potential / Electrostatic Potential (V).
- Relationship Between Electric Field Intensity (E) and Electrostatic Potential (V).
- Electric Potential Due To a Circular Disk.
- Electric Dipole.
- Numericals / Solved Examples - Electric Potential and Electric Dipole.
- Energy Density In Electrostatic Field / Work Done To Assemble Charges.
- Numericals / Solved Examples - Electrostatic Energy and Energy Density.
- Numericals / Solved Examples - Gauss's law...
Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.



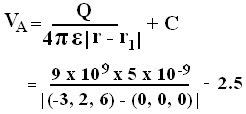










good
ReplyDelete