Properties Of Materials & Electric Current - Electric Fields In Material Space.
- Electric field can not only exist in free space and vacuum but also in any material medium.
- When an electric field is applied to the material, the material will modify the electric field either by strengthening it or weakening it, depending on what kind of material it is.
- Materials are classified into 3 groups based on conductivity / electrical property:
- Conductors (Metals like Copper, Aluminum, etc.) have high conductivity (σ >> 1).
- Insulators / Dielectric (Vacuum, Glass, Rubber, etc.) have low conductivity (σ << 1).
- Semiconductors (Silicon, Germanium, etc.) have intermediate conductivity.
- Conductivity (σ) is a measure of the ability of the material to conduct electricity. It is the reciprocal of resistivity (ρ).
- Units of conductivity are Siemens/meter and mho.
- The basic difference between a conductor and an insulator lies in the amount of free electrons available for conduction of current.
- Conductors have a large amount of free electrons where as insulators have only a few number of electrons for conduction of current.
- Most of the conductors obey ohm’s law. Such conductors are also called ohmic conductors.
- Due to the movement of free charges, several types of electric current can be caused. The different types of electric current are:
- Conduction Current.
- Convection Current.
- Displacement Current.
- Electric current (I) defines the rate at which the net charge passes through a wire of cross sectional surface area S.
Mathematically,
If a net charge ΔQ moves across surface S in some small amount of time Δt, electric current(I) is defined as:
- How fast or how speed the charges will move depends on the nature of the material medium.
- Current density (J) is defined as current ΔI flowing through surface ΔS.
- Imagine surface area ΔS inside a conductor at right angles to the flow of current. As the area approaches zero, the current density at a point is defined as:
The above equation is applicable only when current density (J) is normal to the surface.
- In case if current density(J) is not perpendicular to the surface, consider a small area ds of the conductor at an angle θ to the flow of current as shown:
In this case current flowing through the area is given as:
dI = J dS cosθ = J . dS
I = ∫S (J . dS)
where angle θ is the angle between the normal to the area and direction of the current.
From the above equation it’s clear that electric current is a scalar quantity.
ALSO READ:
- Gauss's Law - Theory.
- Gauss's Law - Application To a Point charge.
- Gauss's Law - Application To An Infinite Line Charge.
- Gauss's Law - Application To An Infinite Sheet Charge.
- Gauss's Law - Application To a Uniformly Charged Sphere.
- Numericals / Solved Examples - Gauss's Law.
- Scalar Electric Potential / Electrostatic Potential (V).
- Relationship Between Electric Field Intensity (E) and Electrostatic Potential (V).
- Electric Potential Due To a Circular Disk.
- Electric Dipole.
- Numericals / Solved Examples - Electric Potential and Electric Dipole.
- Energy Density In Electrostatic Field / Work Done To Assemble Charges.
- Numericals / Solved Examples - Electrostatic Energy and Energy Density.
- Numericals / Solved Examples - Gauss's law...
- Short Notes/FAQ's
Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.
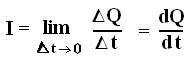


Comments
Post a Comment