Conductors (Isolated & Non-Isolated) In Electric/Electrostatic Field.
- A conductor (such as Copper, Aluminum, gold) contains electrons that are not bounded to the atom and are free to move within the material.
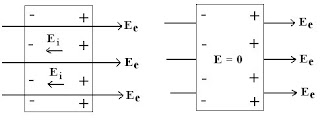
- When an isolated conductor is placed in an external electric field Ee, the negative charges (electrons) starts moving in the opposite direction to that of electric field.
- Soon the electrons get accumulated on the surface of one side of the conductor, while the surface on the other side gets depleted of electrons and hence acquire a positive charge (+ve).
- These separated negative (-ve) and positive charges (+ve) on the opposite sides of the conductor produces an internal induced electric field Ei which opposes the external field Ee inside the conductor.
- If the conductor is a perfect conductor or a good conductor the internal electric field Ei will cancel the external electric field Ee. Hence we can therefore say that
“A perfect conductor cannot contain an electrostatic field inside it.”
- There is a net field of zero magnitude inside the conductor. Hence if E = 0, then the electric flux through any arbitrary closed surface inside the conductor is also equal to zero. This immediately implies that the charge density ρv inside the conductor is equal to zero everywhere (Gauss's law).
- If any excess charge is placed within the volume of the conductor, the repulsive forces pushes them far apart. Since the farthest is the surface itself, all the excess charge resides entirely on the surface. Hence it’s clear that the net charge on an isolated conductor exits only on the surface.
- The electrostatic field at the conductor’s surface is proportional to the surface charge and does not depend on the charge carriers inside the conductor.
- It’s safe to be inside a car / automobile during a thunderstorm. Why?
Ans: Yes, because the metal body of the car carries the excess charge on its external surface. Also we know inside a closed conducting surface electric field is zero. Hence the metal body acts like a screen or shield for the occupants.
PROPERTIES OF AN ISOLATED CONDUCTOR (IN STATIC SITUATION):
- Electric field is zero everywhere within the conductor and also inside a closed conducting surface.
- Any excess charge resides only on the surface of the conductor.
- Electric field just outside the charged conductor is perpendicular to the conductor’s surface.
- On an irregular shaped conductor, the charges tend to accumulate at locations where the radius of curvature of the surface is smallest i.e. at sharp points. Hence we can also say that the field is strongest on the pointy parts of a conductor.
- There is no potential difference between any two points in the conductor i.e. a conductor is an equipotential body.
NON - ISOLATED CONDUCTOR:
OR
CONDUCTOR IN A NON-ELECTROSTATIC EQUILIBRIUM:
- Consider a conductor having a uniform cross section S, length l and whose ends are maintained at a potential difference V as shown in the figure:
- When a potential difference of V is applied across the conductor, the electric field inside a conductor is not zero. Hence there is no static equilibrium inside a conductor.
- A conductor is said to be in electrostatic equilibrium only if no electric field exist inside a conductor.
- Since E ≠ 0, the free charges in the conductor start moving, thus producing conduction current.
- As the electrons moves from one end to another, they experience a damping force called Resistance.
- The electric field E applied is uniform (since V is constant) and is related to electric potential V as:
E = V / l
- Since the conductor has a uniform cross section, the current density is given as:
J = I / S
- Also conduction current density (J) is given as:
J = σ E
- Hence substituting the value of J in the above equation, we have
I = σ E S
Equating the expressions for E
E = V / l = I / σ S
→ V = (l / σ S) I
→ V = I R
- Hence Resistance of a conductor is given as:
R = l / σ S = ρ l / S
Where σ is the conductivity and ρ is the resistivity of the conductor.
- For a conductor of non-uniform cross section , the resistance is given as:
ALSO READ:
- Gauss's Law - Theory.
- Gauss's Law - Application To a Point charge.
- Gauss's Law - Application To An Infinite Line Charge.
- Gauss's Law - Application To An Infinite Sheet Charge.
- Gauss's Law - Application To a Uniformly Charged Sphere.
- Numericals / Solved Examples - Gauss's Law.
- Scalar Electric Potential / Electrostatic Potential (V).
- Relationship Between Electric Field Intensity (E) and Electrostatic Potential (V).
- Electric Potential Due To a Circular Disk.
- Electric Dipole.
- Numericals / Solved Examples - Electric Potential and Electric Dipole.
- Energy Density In Electrostatic Field / Work Done To Assemble Charges.
- Numericals / Solved Examples - Electrostatic Energy and Energy Density.
- Numericals / Solved Examples - Gauss's law...
Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.





Hello, I'm a graduate student in EE. At first, I am appreciated you to your article. It makes me clear up to understand PEC. But I was wondering if I can say “A perfect conductor cannot contain an electric field inside it.” instead of electrostatic.
ReplyDeleteI'd like to get your opinion below email.
hojoong.choi@kaist.ac.kr
Hi Hojoong,
ReplyDeleteNo u cannot say the above statement.
A perfect conductor cannot contain an electrostatic field inside it, but a perfect conductor under the influence of eletromagnetic field, can contain elements of electric field in such a way that eventually they will be cancelling each other's effect.