Solved Examples/Numericals - Gradient Of A Scalar.
Q. 1 Find the gradient of these scalar fields:
a) U = 4xz2 + 3yz
b) H = r2cosθ cosφ
Ans:
a)
=>∇ U = 4z2 ax + 3z ay + (8xz +3y) az
b)
=>∇ H = 2r cosθ cosφ ar + r sinθ cosφ aθ + rcosθ sinφ aφ
Q.2 If V(x, y, z) = 3x2y –y2z2, find ∇ V and |∇ V| at the point (1, 2, -1).
Ans:
∇ V = 6xy ax + (3x2 – 2yz2) ay + (-2y2z) az
At the point (1, 2, -1)
∇ V = 6(1)(2) ax + [3(12) – 2(2)(-1)2] ay – 2(2)2 (-1) az
=>∇ V = 12ax - ay + 8az
|∇ V| (1, 2, -1) = |12ax - ay + 8az | = (209)1/2
Q.3 Given φ = xy +yz +xz, find gradient φ at point (1, 2, 3) and thedirectional derivative of φ
Ans:
∇ φ = (y + z)ax + (x + z)ay + (y + z)az
At point (1, 2, 3)
∇ φ = 5ax + 4ay + 3az
The directional derivative is given as:
dφ/dl = ∇ φ . al
= (5, 4, 3) . [(3, 4, 4) – (1, 2, 3)] / 3
= [(5, 4, 3) . (2, 2, 1)] / 3 = 7
Q.4 Find V(x, y, z) if grad V = (y2 – 2xyz3)ax + (3 + 2xy – x2z3)ay + (4z3 – 3x2yz2)az and V(0, 0, 0) = -2.
Ans:
∂V / ∂x = y2 -2xyz3
∂V / ∂y = 3 + 2xy – x2z3
∂V / ∂y = 4z3 – 3x2yz2
V = ∫( y2 – 2xyz3) dx = xy2 – x2yz3 + f(y, z)
V = ∫( 3 + 2xy – x2z3) dy = 3y + xy2 – x2yz3 + g(x, z)
V = ∫( 4z3 – 3x2yz2) dz = z4 – x2yz3 + h(x, y)
Comparing the above 3 equations, we have
f (x, y) = 3y + z4 + c
Hence,
V = xy2 – x2yz3 + 3y + z4 + c
Since V(0, 0, 0) = -2
V = xy2 – x2yz3 + 3y + z4 – 2
Q.5 Find the unit normal vector of the surface x2 + y2 + z2 = 14 at (-1, 3, 2) ?
Ans:
Here V (x, y, z) = x2 + y2 + z2
∇ V = 2x ax + 2y ay + 2z az
At point (-1, 3, 2)
∇ V = -2ax + 6ay + 4az
|∇ V| = 2(14)1/2
Unit normal vector
an = ∇ V / | ∇ V |
= - ax + 3ay + 2az / (14)1/2
Q.6 The temperature in an auditorium is given by T = x2 + y2 – z. A mosquito located at (1, 1, 2) in the auditorium desires to fly in such a direction that it will get warm as soon as possible. In what direction must it fly?
Ans:
∇ T = 2xax + 2yay - az
At point (1, 1, 2)
∇ T = 2ax + 2ay - az
The mosquito should move in the direction of 2ax + 2ay - az.
ALSO READ:
- Line , Surface and Volume Intergral.
- Del Operator - Definition and Significance.
- Gradient Of a Scalar (∇ V).
- Numericals / Solved Examples - Gradient Of a Scalar.
- Divergence Of a Vector ( ∇ . A ).
- Numericals / Solved Examples - Divergence Of a Vector.
- Curl Of a Vector ( ∇ x A).
- Laplacian Of a Scalar ( ∇2 V).
Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.
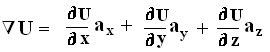


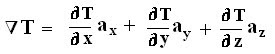



Comments
Post a Comment