Solved Examples/Numericals - Divergence of a Vector Field.
Q.1 Determine the divergence of the following vector fields and evaluate them at the specified points:
a) A = yz ax + 4xy ay + y az at point (1, -2, 3)
Ans:
Given A = yz ax + 4xy ay + y az at point (1, -2, 3)
Divergence of A is given as:
∇ . A = 0 + 4x + 0 = 4x
At Point (1, -2, 3) Hence, ∇ . A = 4
b) A = ρzsinφ aρ + 3ρz2 cosφ aφ at (5, π / 2, 1)
Ans:
Divergence of a vector field A in cylindrical co-ordinate system is given as:
=> ∇ . A = (1/ρ) 2ρz sinφ - (1/ρ) 3ρz2 sinφ
= 2zsinφ - 3z2 sinφ = (2 - 3z) zsinφ
At point (5, π / 2, 1) ∇ . A = (2 – 3) (1) = -1
c) A = 2r cosθ cosφ ar + r1/2 aφ at (1, π / 6, π / 3)
Ans:
Divergence of a vector field A in Spherical co-ordinate system is given as:
=> ∇ . A = (1/r2) 6r2 cosθ cosφ = 6 cosθ cosφ
At point (1, π/6, π/3)
∇ . A= 6 cos π/6 cos π/3 = 2.598.
Q. 2 Determine the flux of D = ρ2 cos2φ aρ + zsin φ aφ over the closed surface of the cylinder, 0 < z < 1, ρ = 4. Verify the divergence theorem for this case.
Ans:
We know a closed cylinder has three surface - top(t), bottom(b) and curved surface(s).
Ψ = Ψt + Ψb + Ψs
Ψt = Ψb = 0, since D has no z component.
It means,
Ψs = ∫ ∫ ρ2 cos2φ (ρ dφ dz)
= ρ3 ∫ 02πcos2φ dφ ∫ 01dz
= (4)3 (π) (1) = 64 π
Therefore,
Ψ = Ψt + Ψb + Ψs = 64 π
By the divergence theorem,
Divergence of D is given as:
∇ . A = 3ρ cos2φ - (1/ρ) cosφ
= ∫ ∫ ∫(3ρ cos2φ - (1/ρ) cosφ) ρdρ dφ dz
= 3 ∫04 ρ2dρ ∫02π cos2φ dφ ∫01dz + ∫04dρ ∫02π cosφdφ ∫01 dz
= 3 (43 /3 ) (π ) (1) = 64π
ALSO READ:
- Line , Surface and Volume Intergral.
- Del Operator - Definition and Significance.
- Gradient Of a Scalar (∇ V).
- Numericals / Solved Examples - Gradient Of a Scalar.
- Divergence Of a Vector ( ∇ . A ).
- Numericals / Solved Examples - Divergence Of a Vector.
- Curl Of a Vector ( ∇ x A).
- Laplacian Of a Scalar ( ∇2 V).
Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.
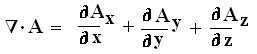



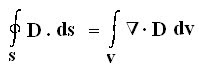






Comments
Post a Comment