Del Operator - Definition & Significance - Coordinate System.


- The collection of partial derivative operators is called DEL operator. Hence DEL can be viewed as the derivative in multi dimensional space.

- DEL operator is defined as a vector differential operator.

- A DEL operator is not a vector in itself, but when acts on a scalar function, it becomes a vector.


- Del is not simply a vector; it is a vector operator. Whereas a vector is an quantity with both a magnitude and direction, DEL does not have a precise value for either until it is allowed to operate on something.

- In Cartesian coordinate system Del operator is given as:



This operator is useful or significant in defining


DEL OPERATOR - CYLINDRICAL CO-ORDINATE SYSTEM:

Unit vectors of Cartesian co-ordinate system are related to unit vectors of Cylindrical co-ordinate system as:

ax = aρ cosφ – aφ sinφ

ay = aρ sinφ + aφ cosφ

az =az

The differential part of x, y in terms of ρ and φ is given as:


Since the del operator is given as:


Substituting the values, we get







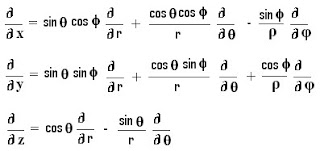
DEL OPERATOR - SPHERICAL CO-ORDINATE SYSTEM:

Unit vectors of Spherical co-ordinate system are related to unit vectors of Cartesian co-ordinate system as:

ax = sinθ cosφ ar + cosθ cosφ aθ – sinφ aφ

ay = sinθ sinφ ar + cosθ sinφ aθ + cosφ aφ

az = cosθ ar - sinθ aθ

The differential part of x, y, z in terms of r, θ and φ as:


Substituting the values, we get







ALSO READ:

- Line , Surface and Volume Intergral.

- Del Operator - Definition and Significance.

- Gradient Of a Scalar (∇ V).

- Numericals / Solved Examples - Gradient Of a Scalar.

- Divergence Of a Vector ( ∇ . A ).

- Numericals / Solved Examples - Divergence Of a Vector.

- Curl Of a Vector ( ∇ x A).

- Laplacian Of a Scalar ( ∇2 V).


Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.

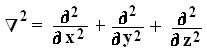
Comments

Post a Comment

Popular posts from this blog

Circular Cylindrical Coordinate System (ρ, φ, z) - Field Theory.

Image
A Vector in Cylindrical system is represented as (A ρ , A φ , A z ) or A = A ρ a ρ + A φ a φ + A z a z Where a ρ , a φ and a z are the unit vectors in ρ, φ and z direction respectively. The physical significance of each parameter of cylindrical coordinates:      - The value ρ indicates the distance of the point from the z-axis. It is the radius of the cylinder .      - The value φ, also called the azimuthal angle , indicates the rotation angle around the z-axis. It is basically measured from the x axis in the x-y plane. It is measured anti-clockwise.      - The value z indicates the distance of the point from z-axis. It is the same as in the Cartesian system. In short, it is the height of the cylinder. Range of the variables: It defines the minimum and the maximum value that ρ, φ and z can have in Cartesian system.  0 ≤ ρ ≤ ∞  0 ≤ φ ≤ 2π - ∞ ≤ z ≤ ∞   Figure shows Point P and Unit vectors in Cylindrical Co-ordinate System. Cylindrical System - Unit v
Read More »

Electric Field Intensity (E) Due To a Circular Ring Charge - Field Theory.

Image
- Consider a circular ring of radius 'a' which carries a uniform line charge density ρ L as shown in figure. - We need to find out electric field at a point P (0, 0, h) on the z axis (z > 0). - Electric field intensity (E) due to any line charge (ρ L ) in general is given as: In this case, dl = a dφ (Since the differential part dl is a differential arc ) R 2 = a 2 + h 2 Consider the triangle shown in the above figure a a ρ + R = h a z → R = - a a ρ + h a z a R = R / | R | a R = - a a ρ + h a z / ( a 2 + h 2 ) 1/2 Substituting all these values in the above equations, the electric field intensity E becomes: - For every element dl there is a corresponding element diametrically opposite that gives an equal but opposite dE ρ so that the two contributions cancel each other. Hence contribution along a ρ due to symmetry adds up to zero. - Therefore the final electric field intensity at point (0, 0, h) has
Read More »

Electric Potential (V) Due To A Uniformly Charged Circular Disc - Field Theory.

Image
- Consider a circular disc of radius ‘a’ which carries a uniform surface charge density ρ s , C /m 2 . - Say the disk lies on x - y plane (or z = 0 plane) with its axis along the z axis as shown in the figure. - We need to find out electric potential (V) due to a circular disk at a point P (0, 0, h) on the z axis (z > 0). - Electric potential (V) at a point due to any surface charge (ρ s ) is given as: - In this case, ds = ρ dρ dφ (Since it’s a disc, the varying terms are radius ρ and angle φ ) R = (ρ 2 + h 2 ) 1/2 - Hence electric potential (V) is given as: - On solving further the equation becomes - As a → 0 , electric potential (V) also tends to zero i.e. V → 0. - Hence the electric potential at point (0, 0, h) is given as: ALSO READ:  - Gauss's Law - Theory. - Gauss's Law - Application To a Point charge. - Gauss's Law - Application To An Infinite Line Charge. - Gauss's
Read More »