Solved Examples / Numericals On Vector Algebra - Field Theory.
Q.1) Given vectors A = ax + 3az and B = 5ax + 2ay -6az, determine
a) |A+B|
b) 5A – B
c) Component of A along ay.
d) Unit vector parallel to 3A + B.
Ans:
a) A + B = ax +3az +5ax +2ay - 6az = 6ax + 2ay – 3az.
|A + B| = (62 + 22 + 32)1/2 = 7.
b) 5A – B = 5(ax + 3az) – 5ax – 2ay + 6az = -2ay + 21az.
c) Component of A along ax, ay and az are 1, 0 and 3 respectively.
d) 3A + B = 3ax + 9az + 5ax + 2ay -6az = 8ax + 2ay +3az
a3A + B = 3A + B/ |3A + B| = (8ax + 2ay + 3az)/ (77)1/2
Q.2) Given Points P (1, -3, 5), Q (2, 4, 6) and R (0, 3, 8) find
a) Position vectors of P and R.
b) Distance vector rQR.
c) Distance between Q and R.
Ans:
a) rp = ax – 3ay + 5az.
rR = 3ay +8az.
b) rQR = rR -rQ
= 3ay +8az – (2ax + 4ay + 6az)
= - 2ax – ay + 2az.
c) |rQR| = (22 + 12 + 22)1/2 = 3.
Q.3) Find the unit vector along the line joining point (2, 4, 4) to point (-3, 2, 2)?
Ans:
Ā = (-3, 2, 2) – (2, 4, 4)
= (-5, -2, -2)
= - 0.87ax - 0.35ay - 0.35az
Q.4) Given that A = 3ax + 5ay – 7az and B = ax – 2ay + az ; find
a) | 2B + 0.4A |
b) A.B - | B |2
c) A x B
Ans:
a) 2B + 0.4A
= 2ax – 4ay +2az + 0.4 (3ax + 5ay – 7az)
= 3.2ax + 6ay - 0.8az
| 2B + 0.4A | = (3.22 + 62 + 0.82)1/2 = 6.846
b) A.B - | B |2
= (3ax + 5ay -7az) . (ax -2ay + az) – (12 + 22 +12)1/2
= - 14 – (6)1/2
= - 16.4494
c) A x B
Q.5) Given Vectors T = 2ax – 6ay + 3az and S = ax + 2ay +az; find
a) the scalar projection of T on S.
b) the vector projection of S on T.
c) the smaller angle between T and S.
Ans:
a)
b)
= -0.286 ax + 0.857ay – 0.43az
c)
Sin θTS = 0.9129 => θTS = 65.91o
Q.6) Let E = 3ay + 4az and F = 4ax – 10ay + 5az
a) Find the component of E along F.
b) Determine a Unit vector perpendicular to both E and F.
Ans:
a)
= - 0.28ax +0.71ay - 0.35az
b)
= ± (0.94, 0.27, -0.21)
Q.7) E and F are vector fields given by E = 2xax + ay +yzaz. and
F = xyax – y2ay +xyzaz. Determine:
a) | E| at (1, 2, 3)
b) Component of E along F at (1, 2, 3)
c) A vector perpendicular to both E and F at (0,1, -3) whose magnitude is unity?
Ans:
a) At (1, 2, 3), E = (2, 1, 6)
b) At (1, 2, 3), F = (2, -4, 6)
= 1.29 ax – 2.57 ay + 3.86 az
c) At (0, 1, -3), E = (0, 1, -3) and F = (0, -1, 0)
ALSO READ:
- Scalars and Vectors.
- Unit Vectors.
- Position and Distance Vectors.
- Vector Multiplication.
- Components Of a Vector.
- Line , Surface and Volume Intergral.
- Del Operator - Definition and Significance.
- Gradient Of a Scalar (∇ V).
- Divergence Of a Vector ( ∇ . A ).
- Curl Of a Vector ( ∇ x A).
- Laplacian Of a Scalar ( ∇2 V).
Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.







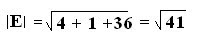





Thank you Sir,
ReplyDeleteFor ur endless effort and dedication to help the students of IACR and others. We bow our heads for ur kind eye to make EMT more easier and conceptual to understand.
Thank You
Soubhagya Mishra
ECE,7th sem
IACR Engg. College.
thank u sir,
ReplyDeletefrom today emt is the easiest subject in iacr. only bcz of you
chinmaya kar
5th sem ECE IACR
Thanks a lot sir !!
ReplyDeletereally nice work done by u!!
will help me a lot !!
once again thanks !!