Line, Surface And Volume Integrals - Field Theory.


- The Line integral of Vector A along a path L is given as

∫L A .dl

- The line integral is the dot product of a vector with a specified curve C.

- We can also say that line integral is the integral of the tangential component of vector A along the curve C.

- If the path of integration is a closed path, the line integral becomes a closed line integral and is called the circulation of A around C.





-  Line Integral is useful in finding the electric field intensity along a path L.

- The surface integral of a vector B across a surface S is defined as

∫s B .ds

- When the surface S is closed, the surface integral becomes the net outward flux of B across S, i.e.







- Surface integral is useful in finding the magnetic flux through a surface S.

- The volume integral of a scalar T over a volume v is given as

∫v T . dv


SOLVED EXAMPLES/NUMERICALS:

Q.1 Calculate the circulation of A = ρ cosφ aρ+ z sinφ az around the edge L of the wedge defined by 0 < ρ < 2, 0 < φ < 60o, z = 0 as shown.













A = ρcosφ aρ+z sinφ az






∫1 A .dl = ∫02 (ρcosφ aρ+zsinφ az) dρaρ = ρ2 cosφ / 2 = 4 / 2 = 2 (since φ = 0o)

∫2 A .dl = ∫0π/3 (ρcosφ aρ + zsinφ az) ρdφaφ = 0

∫3 A .dl = ∫20(ρcosφ aρ+zsinφ az) dρaρ = - 4 cosφ / 2

= -1 (since φ = 60o)






Q.2 Given that H = x2 ax + y2 ay, evaluate ∫L H .dl where L is along the curve y =x2 from (0, 0) to (1, 1).
Ans:
∫L H .dl = ∫( x2 ax + y2 ay ) . (dx ax + dy ay + dz az)
= ∫( x2 dx+ y2 dy )

But on L, y = x2 hence dy = 2x dx

Therefore
∫L H .dl = ∫01[x2 dx+ x4 (2xdx) ] = ∫01( x2 dx+ 2x5 dx )

= | x3/3 |01 + 2 | x6 /6 |01 = 0.667



Q.3 Given that ρs = x2 + xy, calculate ∫s ρsds over the region y ≤ x2, 0< x< 1.
Ans:

∫sρsds = ∫ ∫ x2 dxdy + ∫ ∫ xy dx dy

= ∫01x2 dx ∫dy + ∫01x dx ∫ydy

= ∫01x2 dx | y | + ∫01x dx | y2 / 2 |

= ∫01x4 dx + ∫01 ( x5 / 2) dx = 1/5 + 1/12 = 0.2833



ALSO READ:

- Line , Surface and Volume Intergral.

- Del Operator - Definition and Significance.

- Gradient Of a Scalar (∇ V).

- Numericals / Solved Examples - Gradient Of a Scalar.

- Divergence Of a Vector ( ∇ . A ).

- Numericals / Solved Examples - Divergence Of a Vector.

- Curl Of a Vector ( ∇ x A).

- Laplacian Of a Scalar ( ∇2 V).


Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.

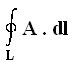
Comments

Post a Comment

Popular posts from this blog

Circular Cylindrical Coordinate System (ρ, φ, z) - Field Theory.

Image
A Vector in Cylindrical system is represented as (A ρ , A φ , A z ) or A = A ρ a ρ + A φ a φ + A z a z Where a ρ , a φ and a z are the unit vectors in ρ, φ and z direction respectively. The physical significance of each parameter of cylindrical coordinates:      - The value ρ indicates the distance of the point from the z-axis. It is the radius of the cylinder .      - The value φ, also called the azimuthal angle , indicates the rotation angle around the z-axis. It is basically measured from the x axis in the x-y plane. It is measured anti-clockwise.      - The value z indicates the distance of the point from z-axis. It is the same as in the Cartesian system. In short, it is the height of the cylinder. Range of the variables: It defines the minimum and the maximum value that ρ, φ and z can have in Cartesian system.  0 ≤ ρ ≤ ∞  0 ≤ φ ≤ 2π - ∞ ≤ z ≤ ∞   Figure shows Point P and Unit vectors in Cyli...
Read More »

Electric Field Intensity (E) Due To a Circular Ring Charge - Field Theory.

Image
- Consider a circular ring of radius 'a' which carries a uniform line charge density ρ L as shown in figure. - We need to find out electric field at a point P (0, 0, h) on the z axis (z > 0). - Electric field intensity (E) due to any line charge (ρ L ) in general is given as: In this case, dl = a dφ (Since the differential part dl is a differential arc ) R 2 = a 2 + h 2 Consider the triangle shown in the above figure a a ρ + R = h a z → R = - a a ρ + h a z a R = R / | R | a R = - a a ρ + h a z / ( a 2 + h 2 ) 1/2 Substituting all these values in the above equations, the electric field intensity E becomes: - For every element dl there is a corresponding element diametrically opposite that gives an equal but opposite dE ρ so that the two contributions cancel each other. Hence contribution along a ρ due to symmetry adds up to zero. - Therefore the final electric field intensity at point (0, 0, h) has ...
Read More »

Electric Potential (V) Due To A Uniformly Charged Circular Disc - Field Theory.

Image
- Consider a circular disc of radius ‘a’ which carries a uniform surface charge density ρ s , C /m 2 . - Say the disk lies on x - y plane (or z = 0 plane) with its axis along the z axis as shown in the figure. - We need to find out electric potential (V) due to a circular disk at a point P (0, 0, h) on the z axis (z > 0). - Electric potential (V) at a point due to any surface charge (ρ s ) is given as: - In this case, ds = ρ dρ dφ (Since it’s a disc, the varying terms are radius ρ and angle φ ) R = (ρ 2 + h 2 ) 1/2 - Hence electric potential (V) is given as: - On solving further the equation becomes - As a → 0 , electric potential (V) also tends to zero i.e. V → 0. - Hence the electric potential at point (0, 0, h) is given as: ALSO READ:  - Gauss's Law - Theory. - Gauss's Law - Application To a Point charge. - Gauss's Law - Application To An Infinite Line Charge. - Gauss's ...
Read More »