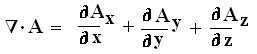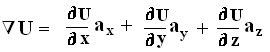ElectroMagnetic Theory Concepts & Solved Numericals

- The laplacian is a scalar operator . Hence when applied to scalar field , the result is also a scalar field. - Laplace operator is a second order differential equation defined as the divergence of the gradient of scalar field. - Laplacian of a scalar field V is written as ∇ 2 V. - Laplacian of a scalar is:             - Used in electrostatics to represent the charge associated to a given potential.             - Used in defining the Helmholtz equation of propagation of EM wave.             - Used in Laplace’s and Poisson’s equation. Laplacian of a scalar field V in Cartesian coordinate system is given as: Laplacian of a scalar field V in Cylindrical coordinate system is given as: Laplacian of a scalar field V in Spherical coordinate system is given as: Q.1 Determi...

Circulation of a vector field A around a closed path L is defined as: Mathematically Curl of a vector A is defined as: Where the area Δ S is bounded by the curve L and the unit vector a n is the unit vector normal to the surface. - The direction of the curl is the axis of rotation , as determined by the right hand thumb rule and the magnitude of the curl is the magnitude of rotation. - From the above relation we can define Curl as the maximum circulation per unit area. - The curl of a vector field provides another vector field that indicates rotational sources of the original vector field. - Curl is a measurement of the circulation of vector field A around a particular point. - If there’s a paper boat in a whirlpool, the circulation would be the amount of force that pushed it along as it went in a circle. The more circulation , the more pushing force you have. - Consider a closed loop counter C. The circulation will be positive if a compone...

Q.1 Determine the divergence of the following vector fields and evaluate them at the specified points: a) A = yz a x + 4xy a y + y a z at point (1, -2, 3) Ans: Given A = yz a x + 4xy a y + y a z at point (1, -2, 3) Divergence of A is given as: ∇ . A = 0 + 4x + 0 = 4x At Point (1, -2, 3)  Hence, ∇ . A = 4 b) A = ρzsinφ a ρ + 3ρz 2 cosφ a φ at (5, π / 2, 1) Ans: Divergence of a vector field A in cylindrical co-ordinate system is given as: => ∇ . A = (1/ρ) 2ρz sinφ - (1/ρ) 3ρz 2 sinφ = 2zsinφ - 3z 2 sinφ =  (2 - 3z) zsinφ At point (5, π / 2, 1)        ∇ . A = (2 – 3) (1) = -1 c) A = 2r cosθ cosφ a r + r 1/2 a φ   at (1, π / 6, π / 3) Ans: Divergence of a vector field A in Spherical co-ordinate system is given as: => ∇ . A = (1/r 2 ) 6r 2 cosθ cosφ = 6 cosθ cosφ At point (1, π/6, π/3) ∇ . A= 6 cos π/6 cos π/3 = 2.598. Q. 2 Determine the flux of D = ρ 2 cos 2 ...

Mathematically divergence of a vector A is defined as: Where the surface S is a closed surface that completely surrounds a small volume Δ v and where ds points outward from the closed surface. - A divergence is applied to a vector as a function of position, yielding a scalar . The divergence actually measures how much the vector function is spreading out. - Divergence of a vector field A is a measure of how much a vector field converges to or diverges from a given point. In simple terms it is a measure of the outgoingness of a vector field. - Divergence of a vector field is positive if the vector diverges or spread out from a given point. If you are at a location from which the vector field tends to point away in all directions, you will definitely have a positive divergence. It means divergence is positive at a source point in the field. - Divergence of a vector field is negative if the vector field converges at that point. If the field points in...

Q. 1 Find the gradient of these scalar fields : a) U = 4xz 2 + 3yz b) H = r 2 cosθ cosφ Ans: a) =>∇ U = 4z 2 a x + 3z a y + (8xz +3y) a z b) =>∇ H = 2r cosθ cosφ a r + r sinθ cosφ a θ + rcosθ sinφ a φ   Q.2 If V (x, y, z) = 3x 2 y –y 2 z 2 , find ∇ V and |∇ V| at the point (1, 2, -1). Ans: ∇ V = 6xy a x + (3x 2 – 2yz 2 ) a y + (-2y 2 z) a z At the point (1, 2, -1) ∇ V = 6(1)(2) a x + [3(12) – 2(2)(-1) 2 ] a y – 2(2) 2 (-1) a z =>∇ V = 12a x - a y + 8a z |∇ V| (1, 2, -1 ) = |12a x - a y + 8a z | = (209) 1/2 Q.3 Given φ = xy +yz +xz, find gradient φ at point (1, 2, 3) and the directional derivative of φ Ans: ∇ φ = (y + z)a x + (x + z)a y + (y + z)a z At point (1, 2, 3) ∇ φ = 5a x + 4a y + 3a z The directional derivative is given as: dφ/dl = ∇ φ . a l = (5, 4, 3) . [(3, 4, 4) – (1, 2, 3)] / 3 = [(5, 4, 3) . (2, 2, 1)] / 3 = 7 Q.4 Find V (x, y, z) if grad V = (y 2 – 2xyz 3 )a x + (3 ...

- The gradient of a scalar field provides a vector field that states how the scalar value is changing throughout space – a change that has both a magnitude and direction. - A gradient is applied to a scalar quantity that is a function of a 3D vector field: position . The gradient measures the direction in which the scalar quantity changes the most, as well as the rate of change with respect to position. - The physical meaning of the gradient of a scalar is that it represents the steepness of the slope or line. For example, height is a scalar quantity; gradient of the height would be a vector pointing upwards. The length of the vector is proportional to the steepness of the slope. - A derivative is required that tells us how fast the function varies , if we move a little distance. - Consider a scalar function T which is a function of space coordinates x, y and z. - The projection or the component of ∇ T in the direction of a unit vector a l is ∇ T . a l and...

- The collection of partial derivative operators is called DEL operator. Hence DEL can be viewed as the derivative in multi dimensional space. - DEL operator is defined as a vector differential operator. - A DEL operator is not a vector in itself, but when acts on a scalar function, it becomes a vector. - Del is not simply a vector ; it is a vector operator. Whereas a vector is an quantity with both a magnitude and direction, DEL does not have a precise value for either until it is allowed to operate on something. - In Cartesian coordinate system Del operator is given as: This operator is useful or significant in defining Gradient of a scalar V (∇ V) Divergence of a vector A (∇ . A) Curl of a vector A (∇ x A) Laplacian of a scalar V (∇ 2 V) DEL OPERATOR - CYLINDRICAL CO-ORDINATE SYSTEM : Unit vectors of Cartesian co-ordinate system are related to unit vectors of Cylindrical co-ordinate system as: a x = a ρ cosφ – a φ sinφ a y = a ρ sinφ + a φ...

- The Line integral of Vector A along a path L is given as ∫ L A .dl - The line integral is the dot product of a vector with a specified curve C. - We can also say that line integral is the integral of the tangential component of vector A along the curve C. - If the path of integration is a closed path, the line integral becomes a closed line integral and is called the circulation of A around C. -  Line Integral is useful in finding the electric field intensity along a path L. - The surface integral of a vector B across a surface S is defined as ∫ s B .ds - When the surface S is closed, the surface integral becomes the net outward flux of B across S, i.e. - Surface integral is useful in finding the magnetic flux through a surface S. - The volume integral of a scalar T over a volume v is given as ∫ v T . dv SOLVED EXAMPLES/NUMERICALS: Q.1 Calculate the circulation of A = ρ cosφ a ρ + z sinφ a z around the edge L of the wedge defin...

Q.1) Given vectors A = a x + 3a z and B = 5a x + 2a y -6a z , determine a) |A+B| b) 5A – B c) Component of A along a y . d) Unit vector parallel to 3A + B. Ans: a) A + B = a x +3a z +5a x +2a y - 6a z = 6a x + 2a y – 3a z . |A + B| = (6 2 + 2 2 + 3 2 ) 1/2 = 7. b) 5A – B = 5(a x + 3a z ) – 5a x – 2a y + 6a z = -2a y + 21a z . c) Component of A along a x , a y and a z are 1 , 0 and 3 respectively. d) 3A + B = 3a x + 9a z + 5a x + 2a y -6a z = 8a x + 2a y +3a z a 3A + B = 3A + B/ |3A + B| = (8a x + 2a y + 3a z )/ (77) 1/2 Q.2) Given Points P (1, -3, 5), Q (2, 4, 6) and R (0, 3, 8) find a) Position vectors of P and R. b) Distance vector r QR . c) Distance between Q and R . Ans: a) r p = a x – 3a y + 5a z . r R = 3a y +8a z . b) r QR = r R -r Q = 3a y +8a z – (2a x + 4a y + 6a z ) = - 2a x – a y + 2a z . c) |r QR | = (2 2 + 1 2 + 2 2 ) 1/2 = 3. Q.3) Find the unit vector along the...