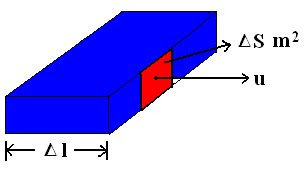
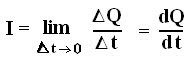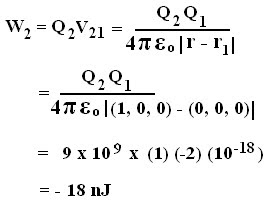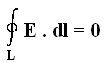Conductors (Isolated & Non-Isolated) In Electric/Electrostatic Field.
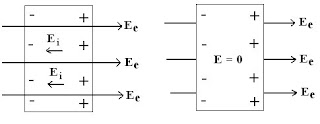
- A conductor (such as Copper, Aluminum, gold) contains electrons that are not bounded to the atom and are free to move within the material. - When an isolated conductor is placed in an external electric field E e , the negative charges ( electrons ) starts moving in the opposite direction to that of electric field. - Soon the electrons get accumulated on the surface of one side of the conductor , while the surface on the other side gets depleted of electrons and hence acquire a positive charge (+ve). - These separated negative (-ve) and positive charges (+ve) on the opposite sides of the conductor produces an internal induced electric field E i which opposes the external field E e inside the conductor. - If the conductor is a perfect conductor or a good conductor the internal electric field E i will cancel the external electric field E e . Hence we can therefore say that “A perfect conductor cannot contain an electrostatic field inside it.” - There ...