Circular Cylindrical Coordinate System (ρ, φ, z) - Field Theory.

A Vector in Cylindrical system is represented as
(A_ρ, A_φ, A_z)
or
A = A_ρa_ρ+ A_φa_φ+ A_za_z

Where a_ρ, a_φand a_z are the unit vectors in ρ, φ and z direction respectively.


The physical significance of each parameter of cylindrical coordinates:

     - The value ρ indicates the distance of the point from the z-axis. It is the radius of the cylinder.

     - The value φ, also called the azimuthal angle, indicates the rotation angle around the z-axis. It is basically measured from the x axis in the x-y plane. It is measured anti-clockwise.


     - The value z indicates the distance of the point from z-axis. It is the same as in the Cartesian system. In short, it is the height of the cylinder.



Range of the variables:

It defines the minimum and the maximum value that ρ, φ and z can have in Cartesian system.

 0 ≤ ρ ≤ ∞
 0 ≤ φ ≤ 2π
-∞ ≤ z ≤ ∞

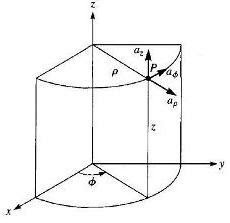
 Figure shows Point P and Unit vectors in Cylindrical Co-ordinate System.



Cylindrical System - Unit vectors:

Since the co-ordinate system is orthogonal, the unit vectors a_ρ, a_φ and a_z are mutually perpendicular to each other.

• a_ρ points in the direction of increasing ρ, i.e a_ρ points away from the z-axis.
• a_φ points in the direction of increasing φ (anticlockwise).
• a_z points in the direction of increasing z.

Relationship between Cylindrical and Cartesian Co-ordinate System Parameters:


Consider the parallelogram ABOC,

X = ρcosφ.
Y = ρsinφ.
Z = Z.

From the above equations we have,




Relationship between (a_x, a_y and a_z) and (a_ρ , a_φand a_z) :

Since a_z is common between the two coordinate system, our main focus is to find out the relation between a_x, a_y and a_ρ , a_φ

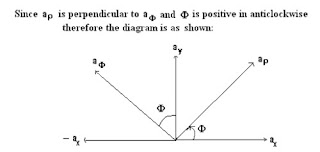
We know φ is the angle from the x-axis on the x-y plane.

From the above figures two equations can be deduced,


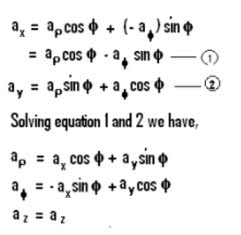
Transformation of vector A from (A_x, A_y, A_z) to (A_ρ, A_φ, A_z) i.e. transformation of Vector A from Cartesian to Cylindrical can be obtained as



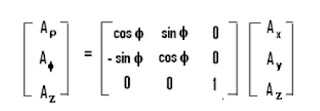
Transformation of vector A from (A_ρ, A_φ, A_z) to (A_x, A_y, A_z) i.e. transformation of Vector A from Cylindrical to Cartesian can be obtained as






SOLVED EXAMPLE / NUMERICAL:

Q.2. Express the point P (1, -4, -3) in cylindrical and spherical co-ordinates? SOLUTION/ANSWER


Q.3
a) If V = XZ – XY +YZ, express V in Cylindrical co-ordinate system.

b) If U = X² + 2Y² +3z², express U in Spherical co- ordinates System.   SOLUTION/ANSWER


Q.4 Transform the vector E = (y² – x²) a_x + xyz a_y + (x² – z²) a_x to cylindrical and spherical system?      SOLUTION/ANSWER


Q.5 Express the vector A = ρ (z² + 1)a_ρ - ρz cosφa_φ in Cartesian co-ordinate system?       SOLUTION/ANSWER


Q.6 Express the vector E =2r sinθ cosφa_r + r cosθ cosφa_θ – r sinφa_φ in Cartesian co-ordinate system?SOLUTION/ANSWER


Q.7 Calculate the distance between the following pair of points?

a) (2, 1, 5) and (6, -1, 2)
b) (3, π/2, -1) and (5, 3π/2, 5)
c) (10, π/4, 3π/4) and (5, π/6, 7π/4)     SOLUTION/ANSWER


ALSO READ:

- Introduction To Coordinate System.

- Cartesian Coordinate System / Rectangular Coordinate System (x, y, z).

- Differential Analysis Of Cartesian Coordinate System.

- Differential Analysis Of Cylindrical Coordinate System.

- Spherical Coordinate System ( r, θ , φ).

- Differential Analysis Of Spherical Coordinate System.

- Numericals / Solved Examples - Page 1.

- Numericals / Solved Examples - Page 2.

- Short Notes/FAQ's

Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.