Cartesian / Rectangular Coordinate System (X, Y, Z) - Field Theory.

A Vector in Cartesian system is represented as
(A_x, A_y, A_z)Or
A = A_xa_x+ A_ya_y+ A_za_z
Where a_x, a_y and a_z are the unit vectors in x, y, z direction respectively.


Range of the variables:

It defines the minimum and the maximum value that x, y and z can have in Cartesian system.

-∞ ≤ x,y,z ≤ ∞

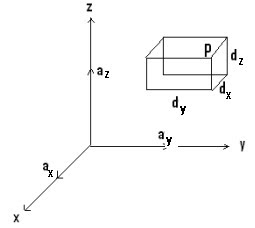
Differential Displacement / Differential Length (dl):

It is given as dl = dxa_x + dya_y + dza_z


Differential length for a surface is given as:

dl = dxa_x + dya_y --- ( For XY Plane or Z Constant Plane).
dl = dya_y + dza_z, ---( For YZ Plane or X Constant Plane).
dl = dxa_x + dza_z ---( For XZ Plane or Y Constant Plane).

Differential length for a line parallel to x, y and z axis are respectively given as:

dl = dxa_x ---( For a line parallel to x-axis).
dl = dya_y ---( For a line Parallel to y-axis).
dl = dza_z, ---( For a line parallel to z-axis).


If there is a wire of length L in z-axis, then the differential length is given as dl = dz a_z. Similarly if the wire is in y-axis then the differential length is given as dl = dy a_y.

Differential Normal Surface (ds):

The differential surface (area element) is defined as ds = ds a_n, where a_n is the unit vector perpendicular to the surface.

For the 1st figure, ds = dydz a_x
2nd figure, ds = dxdz a_y
3rd figure, ds = dxdy a_z

Differential surface is basically a cross product between two parameters of the surface. For example, consider the first figure. The surface has two differential lengths, one is dy and dz. The differential surface (ds) is hence given as:
Where a_n is the unit vector normal to both dy and dz
i.e. a_n = a_y * a_z = a_x

In other words the differential surface element (ds) has an area equal to product dydz, and a normal vector that points in a_x direction.

Differential Volume element (dv)

The differential volume element (dv) can be expressed in terms of the triple product.

dv = dx . (dy * dz)

Consider a cubical surface having dimension x * y * z. The differential volume (dv) of the cubical surface is given as the triple product of the dimensions.

dv = dx . (dy * dz)
= dx a_x . (dy dz a _xsin θ _AB )
= dx a_x . (dy dz a _x)
= dx dy dz

Where dy and dz are mutually perpendicular to each other. Therefore the angle between them is 90^o.

One thing to remember isthat, the three parameters of Cartesian coordinate system i.e. X, Y, Z are all mutually perpendicular to each other.

Therefore a_x, a_y and a_z are all mutually perpendicular to each other.

SOLVED EXAMPLE / NUMERICAL:

Q.1 Express the following points in Cartesian co-ordinate system.
a) P1 (2, 30^o, 5)
b) P2 (4, 30^o, 60^o)                                   SOLUTION/ANSWER


ALSO READ:

- Introduction To Coordinate System.

- Differential Analysis Of Cartesian Coordinate System.

- Circular Cylindrical Coordinate System (ρ, φ, z).

- Differential Analysis Of Cylindrical Coordinate System.

- Spherical Coordinate System ( r, θ , φ).

- Differential Analysis Of Spherical Coordinate System.

- Numericals / Solved Examples - Page 1.

- Numericals / Solved Examples - Page 2.
- Short Notes/FAQ's

Your suggestions and comments are welcome in this section. If you want to share something or if you have some stuff of your own, please do post them in the comments section.