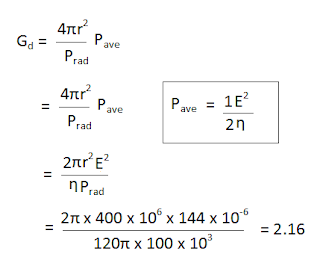
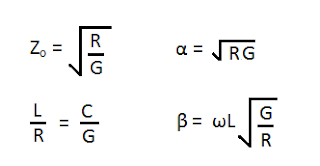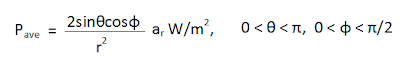Transmission Lines - Solved Numericals / Problems - 2.
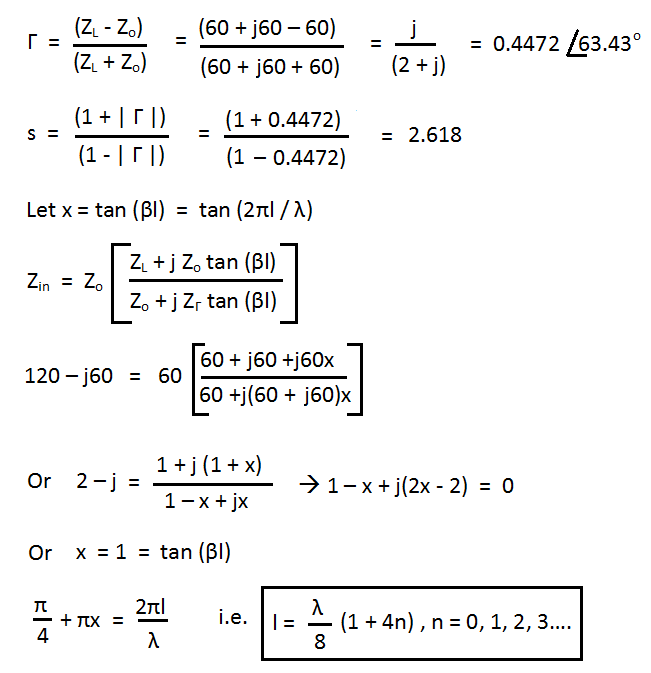
Q.4) A 70 Ω lossless line has s = 1.6 and θ Γ = 300 o . If the line is 0.6λ long, obtain (a) Γ, Z L , Z in (b) The distance of the first minimum voltage from the load Answer: a) Using the smith chart, locate S at s = 1.6. Draw a circle of radius OS. Locate P where θ Γ = 300 o . At P, | Γ | = OP / OQ = 2.1 cm / 9.2 cm = 0.228 Γ = 0.228 ∠300 o Also at P, Z L = 1.15 – j0.48, Z L = Z o Z L = 70 (1.15 – j0.48) = 80.5 – j33.6 Ω l = 0.6 λ = 0.6 x 720 o = 432 o = 360 o + 72 o From P, move 432 o to R. At R, Z in = 0.68 – j0.25 Z in = Z o Z in = 70 (0.68 – j0.25) = 47.6 – j17.5 Ω b) The maximum voltage (the only one) occurs at θ Γ = 180 o ; its distance from the load is (180 – 60) λ / 720 = λ / 6 = 0.1667 Ω Q.5) A lossless 60 Ω line is terminated by a 60 + j60 Ω load. (a) Find Γ and s. If Z in = 120 - j60 Ω, how far (in terms of wavelengths) is the load from the generat...