Solved Exercise/Numericals - Transmission Lines - 1.
Q.1) A transmission line operating at 500 MHz has Zo = 80Ω, α = 0.04Np/m, β = 1.5 rad/m. Find the line parameters R, L, G and C.
Answer:
Since Zo is real & α ǂ 0, this is a distortionless line.
Ro = α Zo = 0.04 x 80 = 3.2 Ω / m
G = α / Zo = 0.04 / 80 = 5 x 10-4 Ω / m
L = β Zo / ω = 1.5 x 80 / (2 π x 5 x 108 ) = 38.2 nH / m
C = L G / R = 38.2 x 10-9 x 5 x 10-4 / 3.2 = 5.97 pF / m
Q.2) A telephone line R = 30 Ω /km, L = 100 mH/km, G = 0 , and C = 20 µF/km. At f = 1 kHz, obtain:
a) The characteristics impedance of the line.
b) The propagation constant.
c) The phase velocity.
Answer:
Q.3) A 40 m long transmission line has Vg = 15 ∠0o Vrms , Zo = 30 + j60 Ω, and VL = 5 ∠-48o Vrms . If the line is matched to the load, calculate:
a) The input impedance Zin
b) The sending end current Iin and voltage Vin
c) The propagation constant γ
Answer:
a) Zg = Z1 --> Zin = Zo = 30 + j60 Ω
b) Vin = Vo = ( Zin / (Zin + Zo) ) Vg = Vg / 2 = 7.5∠0oVrms
Iin = Ip = Vg / (Zg + Zin) = Vg / 2Zo = 15∠0o / 2 (30 + j60o) = 0.05∠-63.43o A
c) Since Zo = Zr, Γ = 0 --> Vo- = 0, Vo+ = Vo
The load voltage is VL = Vs (z = l) = Vo+ e-γl
e-γl = Vo+ / VL = 7.5 ∠0o / 5 ∠ -48o = 1.5 ∠48o
eαl ejβl = 1.5 ∠48o
eαl = 1.5 --> α = (1 / l) ln (1.5) = (1/40) ln (1.5) = 0.0101
ejβl = ej48 --> β = (1 / l) (48o / 180o) π rad = 0.02094
γ = 0.0101 + j0.2094 / m
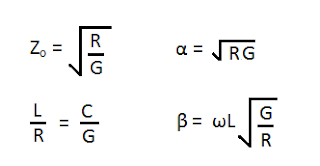





Comments
Post a Comment